計算尺には、指数・対数を計算するための尺が準備されています。
指数・対数を計算するための尺には大きく分けて2種類あります。
計算尺を調べてみてください。どこかにL尺というのがあるはずです。ごくまれに、Ln尺という尺もあるものもあります。このLn尺はL尺の仲間です。
また、ある程度上位の計算尺にはLL尺というのがあります。「LL尺」という尺自体があるものもある計算尺もあるかもしれませんが、たいていはLL0尺、LL1尺、LL2尺、LL3尺、LL00尺、LL01尺、LL02尺、LL03尺となっています。計算尺によってはLL0尺をLL+0尺と表記したり、LL00尺をLL-0尺、あるいはLL/0尺と表記したものもありますが、同じことです。
以下では、個別の尺を指していう場合はLL0尺、LL1尺、LL2尺、LL3尺、LL00尺、LL01尺、LL02尺、LL03尺、これらをまとめていう場合はLL尺ということにします。
なお、単にlogと書いた場合は、底が10の対数、つまりlog10を表すことにします。底がe(=2.718281828…、ネイピアの数、自然対数の底)の対数はlnで表記します。
それでは、10のx乗や、log10のxを求めてみましょう。
これらの値を読み取るには、L尺を使います。
L尺をじっと見つめてください。なんかほかの尺とちょっと違いますよね。ほかの尺は目盛りがだんだん狭くなるなど等間隔に並んでいませんが、L尺は等間隔に目盛りがあります。じつは、L尺はただの直線の尺だったのです。
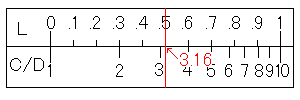
では、100.5を求めてみましょう。固定尺にL尺がある場合はD尺、滑尺にL尺がある場合はC尺と比較します。(滑尺の基線を固定尺の基線に合わせた場合は、C尺、D尺のどちらでも利用することが出来ます。)
まず、L尺の0.5にカーソル線を合わせます。そして、C尺(あるいはD尺)の目盛りを読みます。

すると、答えの3.16を読み取ることが出来ます。
次に、log102を求めてみましょう。
まず、C尺(あるいはD尺)の2にカーソル線を合わせます。そして、L尺の目盛りを読みます。
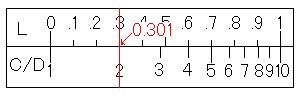
すると、答えの0.301を読み取ることが出来ます。
そもそもC尺やD尺は、log10(x)で目盛りがふってあるのでした。またL尺は直線で目盛りがふってあります。つまり、xという目盛りはC尺の左端からlog(x)の位置に、yという目盛りはL尺の左端からyの位置にあるのです。
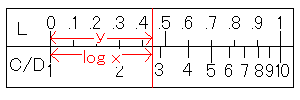
y=log(x)となりますね。これで計算の原理がわかりました。
L尺では底を10とした指数と対数の値を求めることが出来ました。Ln尺を使って、上記とまったく同様の計算をすると、eを底とする指数対数の計算をすることが出来ます。ここでeとはネイピアの数、つまり、自然対数の底で、e=2.718281828…です。
しかし、eを底とする指数対数の計算をする時は、次に述べるLL尺を利用することが多いです。
では、ln(3)を求めてみましょう。まず、LL3尺の3にカーソル線を合わせてください。そして、D尺の目盛りを読んでください。
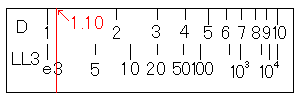
すると、答えの1.10を読むことが出来ます。
では、e1.5を求めてみましょう。まずD尺の1.5にカーソル線を合わせます。そして、LL3尺の目盛りを読みます。
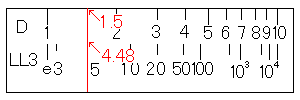
すると、答えの4.48を求めることが出来ます。
実は、LL3尺には、yという目盛りがlog(ln(y))の位置にふってあります。
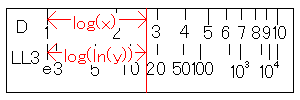
この関係から、log(x)=log(ln(y))、つまり、x=ln(y)となり、自然対数や指数の値を計算することが出来たのです。
LL尺には、LL3尺だけではなく、すべてで、LL0尺、LL1尺、LL2尺、LL3尺、LL00尺、LL01尺、LL02尺、LL03尺と8本あります。これらの目盛りは、受け持つ範囲が違っています。
| 尺の名前 | 尺の目盛りの範囲 | D尺での目盛りの読み |
|---|---|---|
| LL3 | e(2.7)~20000 | 1~10 |
| LL2 | 1.1~e(2.7) | 0.1~1 |
| LL1 | 1.01~1.1 | 0.01~0.1 |
| LL0 | 1.001~1.01 | 0.001~0.01 |
| LL00 | 0.999~0.99 | -0.001~-0.01 |
| LL01 | 0.99~0.91 | -0.01~-0.1 |
| LL02 | 0.91~1/e(0.37) | -0.1~-1 |
| LL03 | 1/e(0.37)~0.00005 | -1~-10 |
先ほどは、LL3尺を利用しました。LL3尺ではD尺の読みが1~10ですので、そのまま目盛りを読みました。もし、LL3尺以外の尺を利用した時は、上の表を参考に、D尺の目盛りを読み変えなければなりません。あとあと利用することになりますので、覚えてしまいましょう。